stem/AI/Neural Networks/MLP/Back-Propagation.md

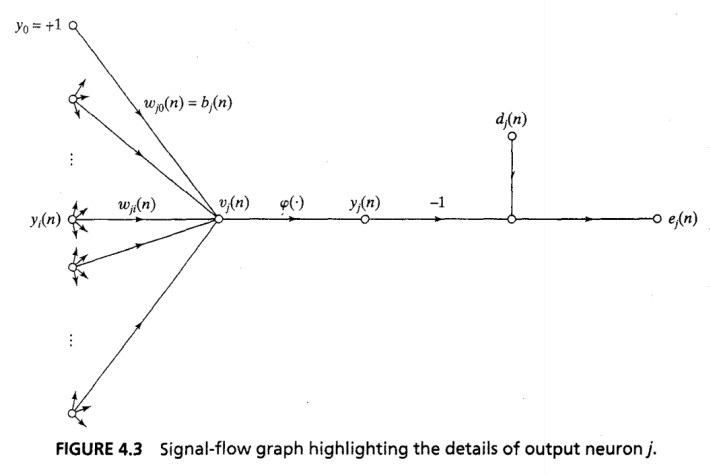
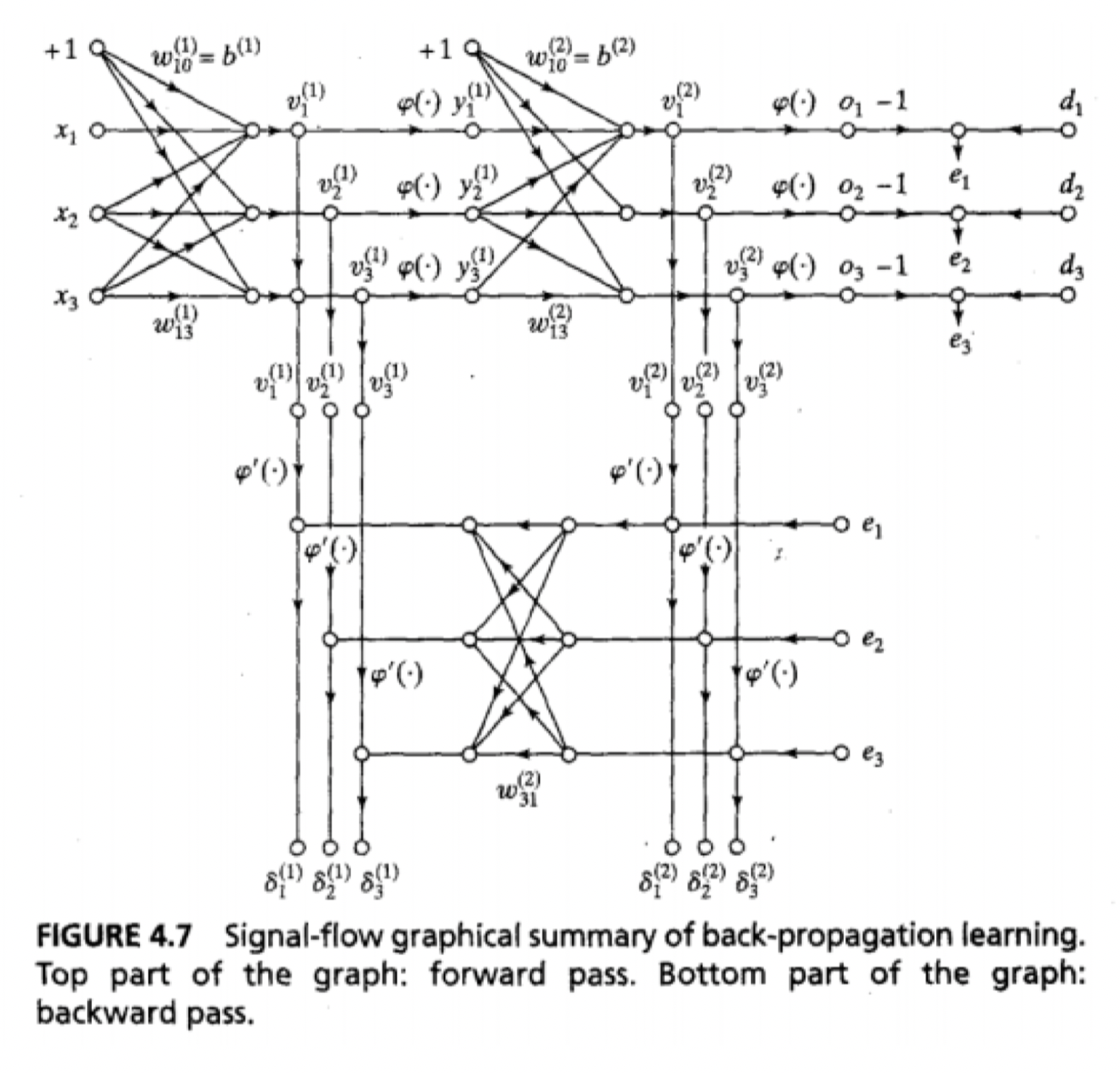
Error signal graph

1. Error Signal
   • e_j(n)=d_j(n)-y_j(n)
2. Net Internal Sum
   • v_j(n)=\sum_{i=0}^mw_{ji}(n)y_i(n)
3. Output
   • y_j(n)=\varphi_j(v_j(n))
4. Instantaneous Sum of Squared Errors
   • \mathfrak{E}(n)=\frac 1 2 \sum_{j\in C}e_j^2(n)
   • C = o/p layer nodes
5. Average Squared Error
   • \mathfrak E_{av}=\frac 1 N\sum_{n=1}^N\mathfrak E (n)

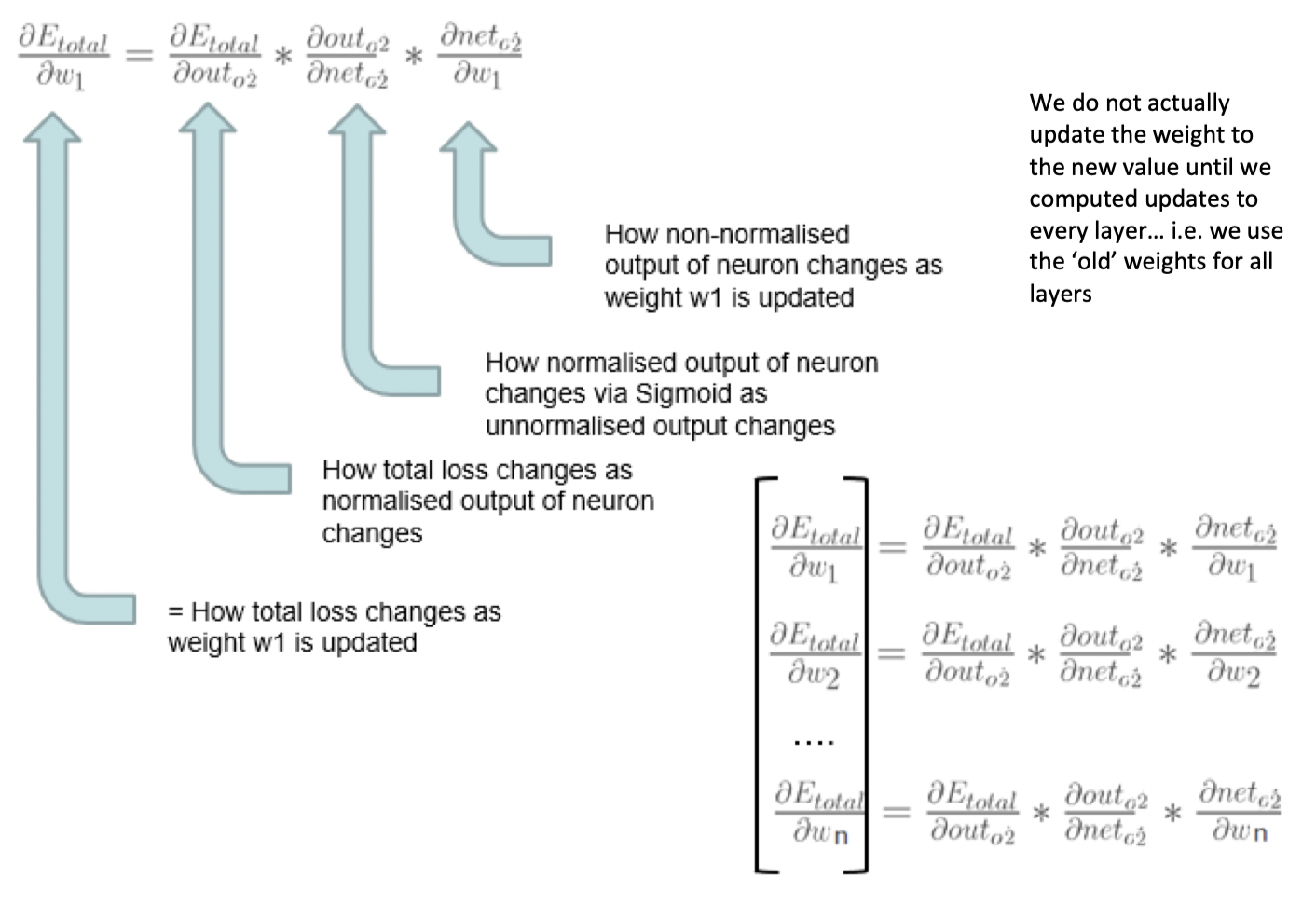
\frac{\partial\mathfrak E(n)}{\partial w_{ji}(n)}=
\frac{\partial\mathfrak E(n)}{\partial e_j(n)}
\frac{\partial e_j(n)}{\partial y_j(n)}
\frac{\partial y_j(n)}{\partial v_j(n)}
\frac{\partial v_j(n)}{\partial w_{ji}(n)}

From 4

\frac{\partial\mathfrak E(n)}{\partial e_j(n)}=e_j(n)

From 1

\frac{\partial e_j(n)}{\partial y_j(n)}=-1

From 3 (note prime)

\frac{\partial y_j(n)}{\partial v_j(n)}=\varphi_j'(v_j(n))

From 2

\frac{\partial v_j(n)}{\partial w_{ji}(n)}=y_i(n)

Composite

\frac{\partial\mathfrak E(n)}{\partial w_{ji}(n)}=
-e_j(n)\cdot
\varphi_j'(v_j(n))\cdot
y_i(n)

\Delta w_{ji}(n)=-\eta\frac{\partial\mathfrak E(n)}{\partial w_{ji}(n)}

\Delta w_{ji}(n)=\eta\delta_j(n)y_i(n)

Gradients

Output Local

\delta_j(n)=-\frac{\partial\mathfrak E (n)}{\partial v_j(n)}

=-\frac{\partial\mathfrak E(n)}{\partial e_j(n)}\frac{\partial e_j(n)}{\partial y_j(n)}\frac{\partial y_j(n){\partial v_j(n)}

=e_j(n)\cdot\varphi_j'(v_j(n))

Hidden Local

\delta_j(n)=-\frac{\partial\mathfrak E (n)}{\partial y_j(n)}\frac{\partial y_j(n)}{\partial v_j(n)}

=-\frac{\partial\mathfrak E (n)}{\partial y_j(n)}\cdot\varphi_j'(v_j(n))

\delta_j(n)=\varphi_j'(v_j(n))\cdot\sum_k \delta_k(n)\cdot w_{kj}(n)

Weight Correction

\text{weight correction = learning rate $\cdot$ local gradient $\cdot$ input signal of neuron $j$}

\Delta w_{ji}(n)=\eta\cdot\delta_j(n)\cdot y_i(n)

• Looking for partial derivative of error with respect to each weight
• 4 partial derivatives
  1. Sum of squared errors WRT error in one output node
  2. Error WRT output y
  3. Output y WRT Pre-activation function sum
  4. Pre-activation function sum WRT weight
     • Other weights constant, goes to zero
     • Leaves just y_i
  • Collect 3 boxed terms as delta j
    • Local gradient
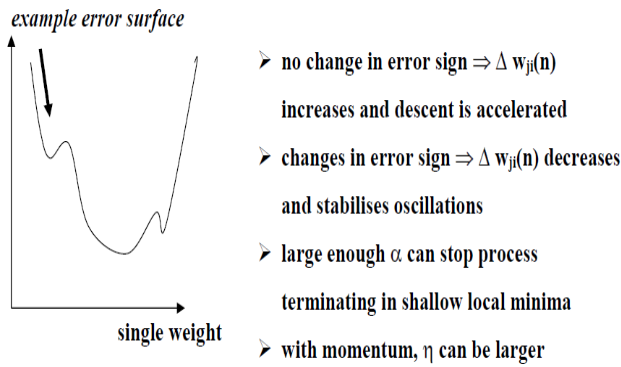
• Weight correction can be too slow raw
  • Gets stuck
  • Add momentum

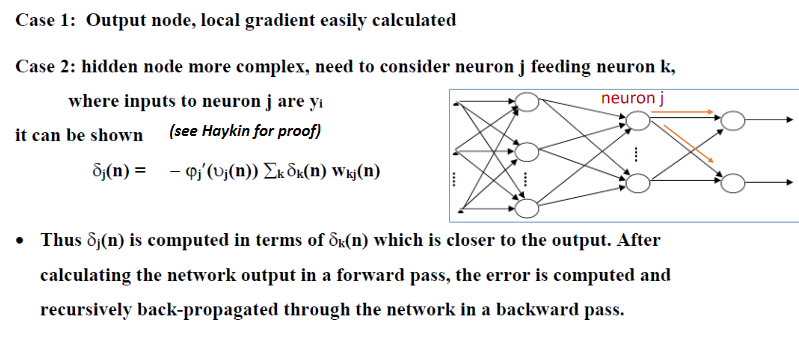
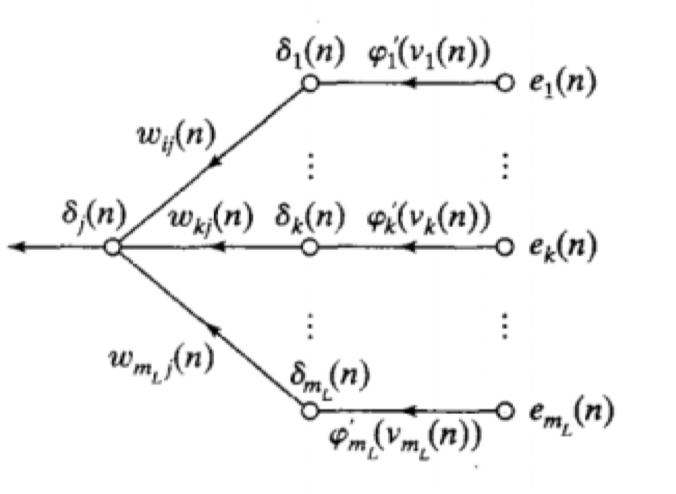
• Nodes further back
  • More complicated
  • Sum of later local gradients multiplied by backward weight (orange)
  • Multiplied by differential of activation function at node

Global Minimum

• Much more complex error surface than least-means-squared
• No guarantees of convergence
  • Non-linear optimisation
• Momentum
  • +\alpha\Delta w_{ji}(n-1), 0\leq|\alpha|<1
  • Proportional to the change in weights last iteration
    • Can shoot past local minima if descending quickly

w^+_5=w_5-\eta\cdot\frac{\partial E_{total}}{\partial w_5}