Affected files: .obsidian/graph.json .obsidian/workspace.json Gaming/Steam controllers.md Gaming/Ubisoft.md STEM/Signal Proc/Convolution.md STEM/Signal Proc/Fourier Transform.md STEM/Signal Proc/Pole-Zero.md STEM/Signal Proc/System Classes.md STEM/Signal Proc/Transfer Function.md STEM/Speech/Linguistics/Consonants.md STEM/Speech/Linguistics/Linguistics.md STEM/Speech/Linguistics/Terms.md STEM/Speech/Linguistics/Vowels.md STEM/Speech/Literature.md STEM/Speech/NLP/Jargon.md STEM/Speech/NLP/NLP.md STEM/Speech/NLP/Recognition.md STEM/Speech/Perception/Perception.md STEM/Speech/Speech Processing/Applications.md STEM/Speech/Speech Processing/Source-Filter.md STEM/Speech/Speech Processing/Vocal Tract.md Work/Applications/Anthropic/Cover letter.md Work/Applications/Anthropic/In line with values.md Work/Applications/Anthropic/Why Work.md Work/Companies.md Work/Freelancing.md Work/Products.md Work/Tech.md
1.6 KiB
1.6 KiB
| tags | |
|---|---|
|
- Poles
- X
- Let
X(z) = inf- Let
1/X(z) = 0
- Let
- Roots of denominator
- Zeros
- O
- Let
X(z) = 0 - Roots of numerator
- In complex (Z for speech) domain
Magnitude Response From Pole/Zeros MIT Pole Zero
Representation of rational transfer function, identifies
- Stability
- Causal/Anti-causal system
- ROC
- Minimum phase/Non minimum phase
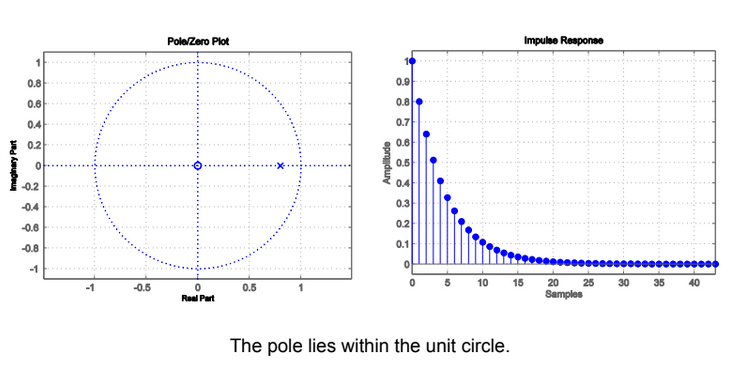
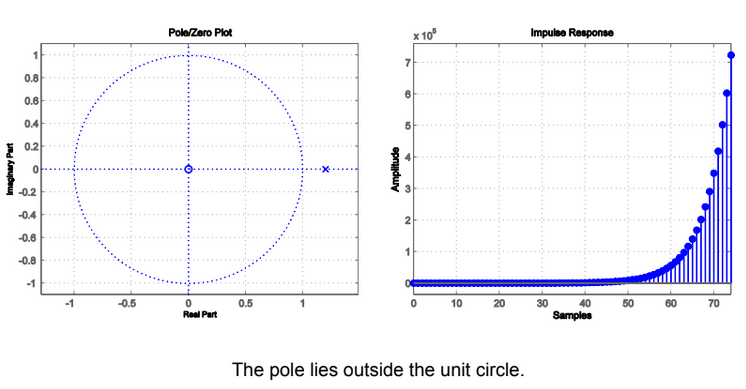
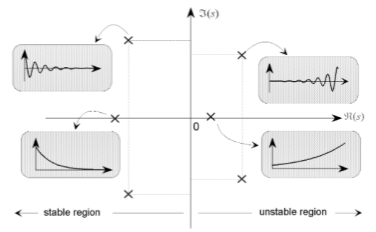
BIBO Stable
- All poles of H must lie within the unit circle of the plot
- If we give an input less than a constant
- Will get an output less than some constant
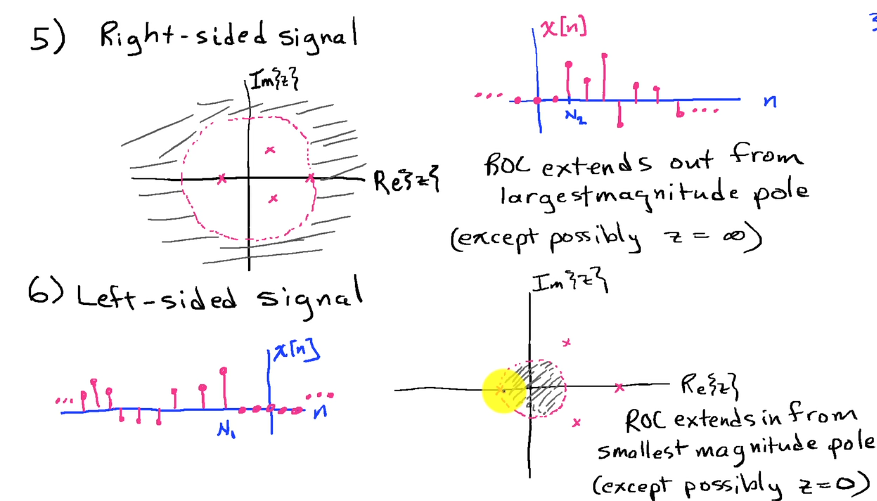
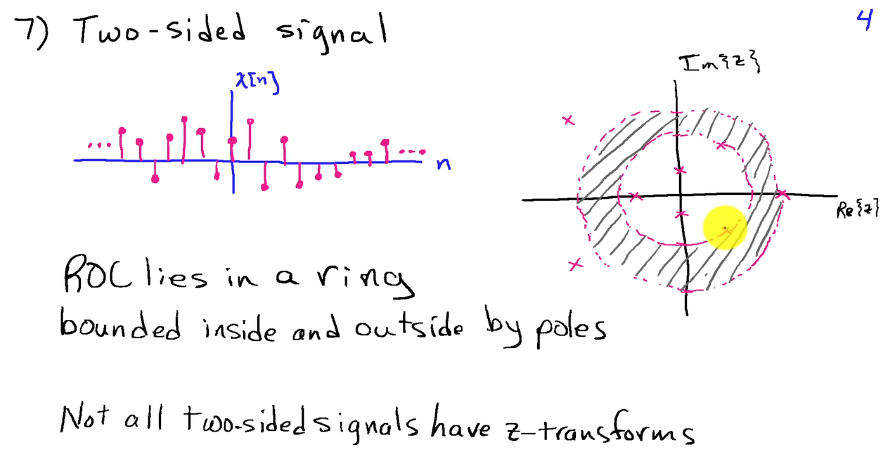
Region of Convergence
- Depends on whether causal or anti-causal
- Cannot contain poles
- Goes to infinity
Continuous
- If includes imaginary axis
- BIBO stable
- All poles must be left of i axis
- Rightwards from pole with largest real-part (not infinity)
- Causal
- Leftward from pole with smallest real-part (not -infinity)
- Anti-causal
Discrete
- If includes unit circle
- BIBO stable
- Outward from pole with largest (not infinite) magnitude
- Right-sided impulse response
- Causal (if no pole at infinity)
- Inward from pole with smallest (nonzero) magnitude
- Anti-causal
Sinusoidal when complex pair
e^{-j\omega}- Euler's for oscillating Exponential when on the axis
- Decays, no $i$ in the exponent