stem/AI/Neural Networks/SLP/Least Mean Square.md

tags
ai maths

• To handle overlapping classes
• Linearity condition remains
  • Linear boundary
• No hard limiter
  • Linear neuron
• Cost function changed to error, J
  • Half doesn’t matter for error
    • Disappears when differentiating

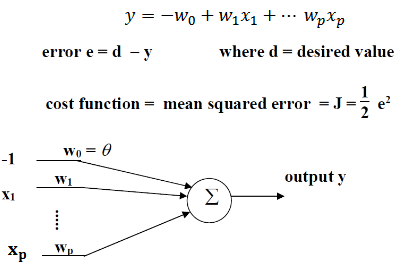
\mathfrak{E}(w)=\frac{1}{2}e^2(n)

• Cost' w.r.t to weights

\frac{\partial\mathfrak{E}(w)}{\partial w}=e(n)\frac{\partial e(n)}{\partial w}

• Calculate error, define delta

e(n)=d(n)-x^T(n)\cdot w(n)

\frac{\partial e(n)}{\partial w(n)}=-x(n)

\frac{\partial \mathfrak{E}(w)}{\partial w(n)}=-x(n)\cdot e(n)

• Gradient vector
  • g=\nabla\mathfrak{E}(w)
  • Estimate via:

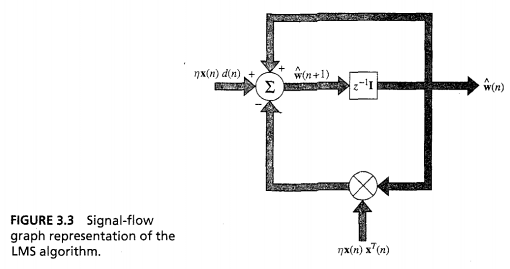
\hat{g}(n)=-x(n)\cdot e(n)

\hat{w}(n+1)=\hat{w}(n)+\eta \cdot x(n) \cdot e(n)

• Above is a feedforward loop around weight vector, \hat{w}
  • Behaves like low-pass filter
    • Pass low frequency components of error signal
  • Average time constant of filtering action inversely proportional to learning-rate
    • Small value progresses algorithm slowly
      • Remembers more
      • Inverse of learning rate is measure of memory of LMS algorithm
• $\hat{w}$ because it's an estimate of the weight vector that would result from steepest descent
  • Steepest descent follows well-defined trajectory through weight space for a given learning rate
  • LMS traces random trajectory
  • Stochastic gradient algorithm
  • Requires no knowledge of environmental statistics

Analysis

• Convergence behaviour dependent on statistics of input vector and learning rate
  • Another way is that for a given dataset, the learning rate is critical
• Convergence of the mean
  • E[\hat{w}(n)]\rightarrow w_0 \text{ as } n\rightarrow \infty
  • Converges to Wiener solution
  • Not helpful
• Convergence in the mean square
  • E[e^2(n)]\rightarrow \text{constant, as }n\rightarrow\infty
• Convergence in the mean square implies convergence in the mean
  • Not necessarily converse

Advantages

• Simple
• Model independent
  • Robust
• Optimal in accordance with H^\infty, minimax criterion
  • If you do not know what you are up against, plan for the worst and optimise
• Was considered an instantaneous approximation of gradient-descent

Disadvantages

• Slow rate of convergence
• Sensitivity to variation in eigenstructure of input
• Typically requires iterations of 10 x dimensionality of the input space
  • Worse with high-d input spaces
• Use steepest descent
• Partial derivatives
• Can be solved by matrix inversion
• Stochastic
  • Random progress
  • Will overall improve

\hat{w}(n+1)=\hat{w}(n)+\eta\cdot x(n)\cdot[d(n)-x^T(n)\cdot\hat w(n)]

=[I-\eta\cdot x(n)x^T(n)]\cdot\hat{w}(n)+\eta\cdot x(n)\cdot d(n)

Where

\hat w(n)=z^{-1}[\hat w(n+1)]

Independence Theory