added structure explanation and probability plot
This commit is contained in:
parent
73e377ff33
commit
9da9a4bae6
920
coursework.lyx
920
coursework.lyx
@ -91,11 +91,11 @@ EEE3037 Nanotechnology Coursework
|
||||
6420013
|
||||
\end_layout
|
||||
|
||||
\begin_layout Section
|
||||
\begin_layout Part
|
||||
Quantum Engineering Design
|
||||
\end_layout
|
||||
|
||||
\begin_layout Subsection
|
||||
\begin_layout Section
|
||||
Structure Design
|
||||
\end_layout
|
||||
|
||||
@ -178,9 +178,9 @@ This energy value will be the same as the total band gap for the well from
|
||||
|
||||
\begin_layout Standard
|
||||
\begin_inset Formula
|
||||
\[
|
||||
\varSigma E_{g}=E_{1h}+E_{g}+E_{1e}\thickapprox0.8eV
|
||||
\]
|
||||
\begin{equation}
|
||||
\varSigma E_{g}=E_{1h}+E_{g}+E_{1e}\thickapprox0.8eV\label{eq:Energy-Gap-Sum}
|
||||
\end{equation}
|
||||
|
||||
\end_inset
|
||||
|
||||
@ -317,7 +317,7 @@ Ga
|
||||
As and as such this was tested first.
|
||||
\end_layout
|
||||
|
||||
\begin_layout Subsubsection
|
||||
\begin_layout Subsection
|
||||
Lattice Match
|
||||
\end_layout
|
||||
|
||||
@ -494,7 +494,7 @@ In order to compute a compound lattice constant for InGaAs, Vegard's law
|
||||
\begin_layout Standard
|
||||
\begin_inset Formula
|
||||
\[
|
||||
\alpha_{A_{(1-x)}B_{x}}=(1-x)\alpha_{A}+x\alpha_{B}
|
||||
\alpha_{A_{(1-x)}B_{x}}=\left(1-x\right)\alpha_{A}+x\alpha_{B}
|
||||
\]
|
||||
|
||||
\end_inset
|
||||
@ -522,18 +522,916 @@ This shows that to 4 significant figures the composition of InGaAs is lattice
|
||||
matched to InP to within 0.001Å which is sufficient for this application.
|
||||
\end_layout
|
||||
|
||||
\begin_layout Subsubsection
|
||||
\begin_layout Subsection
|
||||
Band Gap
|
||||
\end_layout
|
||||
|
||||
\begin_layout Subsection
|
||||
Probability Plot
|
||||
\begin_layout Standard
|
||||
Vegard's law can also be used to approximate the band gap of a ternary alloy,
|
||||
such as InGaAs.
|
||||
The band gaps at 300K for each alloy can be seen in table
|
||||
\begin_inset CommandInset ref
|
||||
LatexCommand ref
|
||||
reference "tab:Band-gaps"
|
||||
plural "false"
|
||||
caps "false"
|
||||
noprefix "false"
|
||||
|
||||
\end_inset
|
||||
|
||||
.
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
\begin_inset Float table
|
||||
wide false
|
||||
sideways false
|
||||
status open
|
||||
|
||||
\begin_layout Plain Layout
|
||||
\align center
|
||||
\begin_inset Tabular
|
||||
<lyxtabular version="3" rows="4" columns="2">
|
||||
<features tabularvalignment="middle">
|
||||
<column alignment="center" valignment="top">
|
||||
<column alignment="center" valignment="top">
|
||||
<row>
|
||||
<cell alignment="center" valignment="top" topline="true" bottomline="true" leftline="true" usebox="none">
|
||||
\begin_inset Text
|
||||
|
||||
\begin_layout Plain Layout
|
||||
Material
|
||||
\end_layout
|
||||
|
||||
\end_inset
|
||||
</cell>
|
||||
<cell alignment="center" valignment="top" topline="true" bottomline="true" leftline="true" rightline="true" usebox="none">
|
||||
\begin_inset Text
|
||||
|
||||
\begin_layout Plain Layout
|
||||
Band Gap at 300K, E
|
||||
\begin_inset script subscript
|
||||
|
||||
\begin_layout Plain Layout
|
||||
g
|
||||
\end_layout
|
||||
|
||||
\end_inset
|
||||
|
||||
(eV)
|
||||
\end_layout
|
||||
|
||||
\end_inset
|
||||
</cell>
|
||||
</row>
|
||||
<row>
|
||||
<cell alignment="center" valignment="top" topline="true" leftline="true" usebox="none">
|
||||
\begin_inset Text
|
||||
|
||||
\begin_layout Plain Layout
|
||||
InAs
|
||||
\end_layout
|
||||
|
||||
\end_inset
|
||||
</cell>
|
||||
<cell alignment="center" valignment="top" topline="true" leftline="true" rightline="true" usebox="none">
|
||||
\begin_inset Text
|
||||
|
||||
\begin_layout Plain Layout
|
||||
0.35
|
||||
\end_layout
|
||||
|
||||
\end_inset
|
||||
</cell>
|
||||
</row>
|
||||
<row>
|
||||
<cell alignment="center" valignment="top" topline="true" leftline="true" usebox="none">
|
||||
\begin_inset Text
|
||||
|
||||
\begin_layout Plain Layout
|
||||
GaAs
|
||||
\end_layout
|
||||
|
||||
\end_inset
|
||||
</cell>
|
||||
<cell alignment="center" valignment="top" topline="true" leftline="true" rightline="true" usebox="none">
|
||||
\begin_inset Text
|
||||
|
||||
\begin_layout Plain Layout
|
||||
1.42
|
||||
\end_layout
|
||||
|
||||
\end_inset
|
||||
</cell>
|
||||
</row>
|
||||
<row>
|
||||
<cell alignment="center" valignment="top" topline="true" bottomline="true" leftline="true" usebox="none">
|
||||
\begin_inset Text
|
||||
|
||||
\begin_layout Plain Layout
|
||||
InP
|
||||
\end_layout
|
||||
|
||||
\end_inset
|
||||
</cell>
|
||||
<cell alignment="center" valignment="top" topline="true" bottomline="true" leftline="true" rightline="true" usebox="none">
|
||||
\begin_inset Text
|
||||
|
||||
\begin_layout Plain Layout
|
||||
1.34
|
||||
\end_layout
|
||||
|
||||
\end_inset
|
||||
</cell>
|
||||
</row>
|
||||
</lyxtabular>
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\begin_layout Plain Layout
|
||||
\begin_inset Caption Standard
|
||||
|
||||
\begin_layout Plain Layout
|
||||
Band gaps for prospective well and barrier materials
|
||||
\begin_inset CommandInset citation
|
||||
LatexCommand cite
|
||||
key "new_semiconductor_materials_archive"
|
||||
literal "false"
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\begin_inset CommandInset label
|
||||
LatexCommand label
|
||||
name "tab:Band-gaps"
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
In this case the band gap approximates to,
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
\begin_inset Formula
|
||||
\[
|
||||
E_{g,In_{0.53}Ga_{0.47}As}\thickapprox0.53\cdotp0.35+0.47\cdotp1.42\thickapprox0.85\unit{eV}
|
||||
\]
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
However the band gap has been experimentally found to be 0.75eV
|
||||
\begin_inset CommandInset citation
|
||||
LatexCommand cite
|
||||
key "aip_complete10.1063/1.322570"
|
||||
literal "false"
|
||||
|
||||
\end_inset
|
||||
|
||||
.
|
||||
This implies that the linear relationship provided by Vegard's law is not
|
||||
accurate enough and in this case a modified version including a bowing
|
||||
parameter
|
||||
\begin_inset Formula $b$
|
||||
\end_inset
|
||||
|
||||
should be used,
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
\begin_inset Formula
|
||||
\[
|
||||
E_{g,total}=xE_{g,a}+\left(1-x\right)E_{g,b}-bx\left(1-x\right)
|
||||
\]
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
For this application, however, the experimentally determined value will
|
||||
be used.
|
||||
This value is ideal for this application as it is comparable to and slightly
|
||||
lower than the required 0.8eV energy value.
|
||||
\end_layout
|
||||
|
||||
\begin_layout Subsection
|
||||
Width Calculation
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
Having found two materials that are lattice matched with a suitable band
|
||||
gap value, the final calculation is that of the quantum well width.
|
||||
In order to calculate this value, the equation for energy levels within
|
||||
an infinite quantum well will be used,
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
|
||||
\emph on
|
||||
\begin_inset Formula
|
||||
\begin{equation}
|
||||
E_{n}=\frac{n^{2}\pi^{2}\text{ħ}^{2}}{2mL^{2}}\label{eq:Energy-levels}
|
||||
\end{equation}
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
Referring back to equation
|
||||
\begin_inset CommandInset ref
|
||||
LatexCommand ref
|
||||
reference "eq:Energy-Gap-Sum"
|
||||
plural "false"
|
||||
caps "false"
|
||||
noprefix "false"
|
||||
|
||||
\end_inset
|
||||
|
||||
, the terms for the first electron and hole energy levels can each be replaced
|
||||
with equation
|
||||
\begin_inset CommandInset ref
|
||||
LatexCommand ref
|
||||
reference "eq:Energy-levels"
|
||||
plural "false"
|
||||
caps "false"
|
||||
noprefix "false"
|
||||
|
||||
\end_inset
|
||||
|
||||
as seen below,
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
\begin_inset Formula
|
||||
\[
|
||||
\varSigma E_{g}=0.8\unit{eV}=E_{1h}+E_{g}+E_{1e}=\frac{1^{2}\pi^{2}\text{\emph{ħ}}^{2}}{2m_{h}^{*}L^{2}}+E_{g}+\frac{1^{2}\pi^{2}\text{\emph{ħ}}^{2}}{2m_{e}^{*}L^{2}}
|
||||
\]
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
With the experimentally determined value for
|
||||
\begin_inset Formula $E_{g}$
|
||||
\end_inset
|
||||
|
||||
this equation can be condensed to,
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
\begin_inset Formula
|
||||
\[
|
||||
0.8\unit{eV}=\frac{\pi^{2}\text{\emph{ħ}}^{2}}{2m_{h}^{*}L^{2}}+0.75+\frac{\pi^{2}\text{\emph{ħ}}^{2}}{2m_{e}^{*}L^{2}}
|
||||
\]
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
\begin_inset Formula
|
||||
\[
|
||||
0.05\unit{eV}=\frac{\pi^{2}\text{\emph{ħ}}^{2}}{2L^{2}}\left(\frac{1}{m_{h}^{*}}+\frac{1}{m_{e}^{*}}\right)
|
||||
\]
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
\begin_inset Formula
|
||||
\[
|
||||
L=\sqrt{\frac{\pi^{2}\text{\emph{ħ}}^{2}}{2\cdotp(0.05\unit{eV})}\cdotp\left(\frac{1}{m_{h}^{*}}+\frac{1}{m_{e}^{*}}\right)}
|
||||
\]
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
As a frequently studied composition due to it's favourable structural parameters
|
||||
with InP, The charge carrier effective masses of In
|
||||
\begin_inset script subscript
|
||||
|
||||
\begin_layout Plain Layout
|
||||
0.53
|
||||
\end_layout
|
||||
|
||||
\end_inset
|
||||
|
||||
Ga
|
||||
\begin_inset script subscript
|
||||
|
||||
\begin_layout Plain Layout
|
||||
0.47
|
||||
\end_layout
|
||||
|
||||
\end_inset
|
||||
|
||||
As have been found experimentally to be as shown in table
|
||||
\begin_inset CommandInset ref
|
||||
LatexCommand ref
|
||||
reference "tab:Effective-masses"
|
||||
plural "false"
|
||||
caps "false"
|
||||
noprefix "false"
|
||||
|
||||
\end_inset
|
||||
|
||||
.
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
\begin_inset Float table
|
||||
wide false
|
||||
sideways false
|
||||
status open
|
||||
|
||||
\begin_layout Plain Layout
|
||||
\align center
|
||||
\begin_inset Tabular
|
||||
<lyxtabular version="3" rows="4" columns="2">
|
||||
<features tabularvalignment="middle">
|
||||
<column alignment="center" valignment="top">
|
||||
<column alignment="center" valignment="top">
|
||||
<row>
|
||||
<cell alignment="center" valignment="top" topline="true" bottomline="true" leftline="true" usebox="none">
|
||||
\begin_inset Text
|
||||
|
||||
\begin_layout Plain Layout
|
||||
Charge Carrier
|
||||
\end_layout
|
||||
|
||||
\end_inset
|
||||
</cell>
|
||||
<cell alignment="center" valignment="top" topline="true" bottomline="true" leftline="true" rightline="true" usebox="none">
|
||||
\begin_inset Text
|
||||
|
||||
\begin_layout Plain Layout
|
||||
Effective mass ratio in In
|
||||
\begin_inset script subscript
|
||||
|
||||
\begin_layout Plain Layout
|
||||
0.53
|
||||
\end_layout
|
||||
|
||||
\end_inset
|
||||
|
||||
Ga
|
||||
\begin_inset script subscript
|
||||
|
||||
\begin_layout Plain Layout
|
||||
0.47
|
||||
\end_layout
|
||||
|
||||
\end_inset
|
||||
|
||||
As (
|
||||
\begin_inset Formula $\frac{m^{*}}{m^{0}}$
|
||||
\end_inset
|
||||
|
||||
)
|
||||
\end_layout
|
||||
|
||||
\end_inset
|
||||
</cell>
|
||||
</row>
|
||||
<row>
|
||||
<cell alignment="center" valignment="top" topline="true" leftline="true" usebox="none">
|
||||
\begin_inset Text
|
||||
|
||||
\begin_layout Plain Layout
|
||||
Electron
|
||||
\end_layout
|
||||
|
||||
\end_inset
|
||||
</cell>
|
||||
<cell alignment="center" valignment="top" topline="true" leftline="true" rightline="true" usebox="none">
|
||||
\begin_inset Text
|
||||
|
||||
\begin_layout Plain Layout
|
||||
0.041
|
||||
\begin_inset CommandInset citation
|
||||
LatexCommand cite
|
||||
key "aip_complete10.1063/1.90860"
|
||||
literal "false"
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\end_inset
|
||||
</cell>
|
||||
</row>
|
||||
<row>
|
||||
<cell alignment="center" valignment="top" topline="true" leftline="true" usebox="none">
|
||||
\begin_inset Text
|
||||
|
||||
\begin_layout Plain Layout
|
||||
Light Hole
|
||||
\end_layout
|
||||
|
||||
\end_inset
|
||||
</cell>
|
||||
<cell alignment="center" valignment="top" topline="true" leftline="true" rightline="true" usebox="none">
|
||||
\begin_inset Text
|
||||
|
||||
\begin_layout Plain Layout
|
||||
0.051
|
||||
\begin_inset CommandInset citation
|
||||
LatexCommand cite
|
||||
key "aip_complete10.1063/1.92393"
|
||||
literal "false"
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\end_inset
|
||||
</cell>
|
||||
</row>
|
||||
<row>
|
||||
<cell alignment="center" valignment="top" topline="true" bottomline="true" leftline="true" usebox="none">
|
||||
\begin_inset Text
|
||||
|
||||
\begin_layout Plain Layout
|
||||
Heavy Hole
|
||||
\end_layout
|
||||
|
||||
\end_inset
|
||||
</cell>
|
||||
<cell alignment="center" valignment="top" topline="true" bottomline="true" leftline="true" rightline="true" usebox="none">
|
||||
\begin_inset Text
|
||||
|
||||
\begin_layout Plain Layout
|
||||
0.2
|
||||
\begin_inset CommandInset citation
|
||||
LatexCommand cite
|
||||
key "aip_complete10.1063/1.101816"
|
||||
literal "false"
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\end_inset
|
||||
</cell>
|
||||
</row>
|
||||
</lyxtabular>
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\begin_layout Plain Layout
|
||||
\begin_inset Caption Standard
|
||||
|
||||
\begin_layout Plain Layout
|
||||
Effective masses of charge carriers in
|
||||
\begin_inset CommandInset label
|
||||
LatexCommand label
|
||||
name "tab:Effective-masses"
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
As the electrical and optical properties of the valence band are governed
|
||||
by the heavy hole interactions, this effective mass ration will be used.
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
Substituting these ratios into the above provides,
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
\begin_inset Formula
|
||||
\[
|
||||
L=\sqrt{\frac{\pi^{2}\text{\emph{ħ}}^{2}}{2\cdotp(0.05\unit{eV})\cdotp m_{e}}\cdotp\left(\frac{1}{0.2}+\frac{1}{0.041}\right)}
|
||||
\]
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
which reduces to a well length of 14.87nm.
|
||||
\end_layout
|
||||
|
||||
\begin_layout Subsection
|
||||
Energy Level Calculations
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
With all the parameters of the well ascertained the first and second confined
|
||||
electron and hole energy levels can be found by utilising equation
|
||||
\begin_inset CommandInset ref
|
||||
LatexCommand ref
|
||||
reference "eq:Energy-levels"
|
||||
plural "false"
|
||||
caps "false"
|
||||
noprefix "false"
|
||||
|
||||
\end_inset
|
||||
|
||||
.
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
For confined electron states:
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
|
||||
\emph on
|
||||
\begin_inset Formula
|
||||
\[
|
||||
E_{1e}=\frac{1^{2}\pi^{2}\text{\emph{ħ}}^{2}}{2\cdotp m_{e}^{*}\cdotp\left(14.87\unit{nm}\right)^{2}}
|
||||
\]
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
|
||||
\emph on
|
||||
\begin_inset Formula
|
||||
\[
|
||||
E_{1e}=6.65\times10^{-21}\unit{J}=0.041\unit{eV}
|
||||
\]
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
This equation shows that energy values are proportional to the square of
|
||||
|
||||
\begin_inset Formula $n$
|
||||
\end_inset
|
||||
|
||||
, the principal quantum number or energy level.
|
||||
As such:
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
\begin_inset Formula
|
||||
\[
|
||||
E_{2e}=2^{2}\cdotp E_{1e}
|
||||
\]
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
|
||||
\emph on
|
||||
\begin_inset Formula
|
||||
\[
|
||||
E_{2e}=2.66\times10^{-20}\unit{J}=0.17\unit{eV}
|
||||
\]
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
For confined hole states:
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
|
||||
\emph on
|
||||
\begin_inset Formula
|
||||
\[
|
||||
E_{1h}=\frac{1^{2}\pi^{2}\text{\emph{ħ}}^{2}}{2\cdotp m_{h}^{*}\cdotp\left(14.87\unit{nm}\right)^{2}}
|
||||
\]
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
|
||||
\emph on
|
||||
\begin_inset Formula
|
||||
\[
|
||||
E_{1h}=1.36\times10^{-21}\unit{J}=0.0085\unit{eV}
|
||||
\]
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
\begin_inset Formula
|
||||
\[
|
||||
E_{2h}=2^{2}\cdotp E_{1h}
|
||||
\]
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
|
||||
\emph on
|
||||
\begin_inset Formula
|
||||
\[
|
||||
E_{2h}=5.45\times10^{-21}\unit{J}=0.034\unit{eV}
|
||||
\]
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\begin_layout Section
|
||||
Probability Plot
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
The probability of finding an electron in a quantum well is given by
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
\begin_inset Formula
|
||||
\begin{equation}
|
||||
P=\int_{0}^{L}\psi^{*}\psi dx\label{eq:wave-function-probability}
|
||||
\end{equation}
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
with
|
||||
\begin_inset Formula $\psi$
|
||||
\end_inset
|
||||
|
||||
in the case of an infinite quantum well being given by,
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
\begin_inset Formula
|
||||
\[
|
||||
\psi\left(x\right)=A\sin\left(kx\right)=A\sin\left(\frac{n\pi}{L}x\right)
|
||||
\]
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
Where
|
||||
\begin_inset Formula $A$
|
||||
\end_inset
|
||||
|
||||
acts as a normalisation constant to satisfy the conditions
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
\begin_inset Formula
|
||||
\[
|
||||
\int_{{\textstyle all\:space}}\psi^{*}\psi dV=1
|
||||
\]
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
in this case providing the wave function
|
||||
\begin_inset Formula $\psi$
|
||||
\end_inset
|
||||
|
||||
as
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
\begin_inset Formula
|
||||
\begin{equation}
|
||||
\psi\left(x\right)=\sqrt{\frac{2}{L}}\sin\left(\frac{n\pi}{L}x\right)\label{eq:wave-function}
|
||||
\end{equation}
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
Importantly, the above conditions are for an infinite quantum well where
|
||||
an assumption is made that the well has a barrier region of infinite potential
|
||||
such that the wavefunction is confined to the well.
|
||||
A real quantum well is unable to satisfy this leading to the wavefunction
|
||||
|
||||
\begin_inset Quotes eld
|
||||
\end_inset
|
||||
|
||||
spilling
|
||||
\begin_inset Quotes erd
|
||||
\end_inset
|
||||
|
||||
into the barrier region.
|
||||
For the purposes of plotting the probability density, however, it is a
|
||||
reasonable assumption to make.
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
Considering equation
|
||||
\begin_inset CommandInset ref
|
||||
LatexCommand ref
|
||||
reference "eq:wave-function-probability"
|
||||
plural "false"
|
||||
caps "false"
|
||||
noprefix "false"
|
||||
|
||||
\end_inset
|
||||
|
||||
, if the probability can be found by integrating
|
||||
\begin_inset Formula $\psi^{*}\psi$
|
||||
\end_inset
|
||||
|
||||
, or in this situation
|
||||
\begin_inset Formula $\psi^{2}$
|
||||
\end_inset
|
||||
|
||||
then the probability can be shown by plotting
|
||||
\begin_inset Formula $\psi^{2}$
|
||||
\end_inset
|
||||
|
||||
, see figure
|
||||
\begin_inset CommandInset ref
|
||||
LatexCommand ref
|
||||
reference "fig:Probability-plot"
|
||||
plural "false"
|
||||
caps "false"
|
||||
noprefix "false"
|
||||
|
||||
\end_inset
|
||||
|
||||
.
|
||||
Here the well stretches from 0 to the blue line along the
|
||||
\begin_inset Formula $x$
|
||||
\end_inset
|
||||
|
||||
axis and
|
||||
\begin_inset Formula $n$
|
||||
\end_inset
|
||||
|
||||
has been set to 1 for the ground state.
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
\begin_inset Float figure
|
||||
wide false
|
||||
sideways false
|
||||
status open
|
||||
|
||||
\begin_layout Plain Layout
|
||||
\align center
|
||||
\begin_inset Graphics
|
||||
filename probability-plot.png
|
||||
lyxscale 30
|
||||
width 100col%
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\begin_layout Plain Layout
|
||||
\begin_inset Caption Standard
|
||||
|
||||
\begin_layout Plain Layout
|
||||
Probability plot for electron in ground state
|
||||
\begin_inset CommandInset label
|
||||
LatexCommand label
|
||||
name "fig:Probability-plot"
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\begin_layout Plain Layout
|
||||
|
||||
\end_layout
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\begin_layout Section
|
||||
Probability Intervals
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
Combining equations
|
||||
\begin_inset CommandInset ref
|
||||
LatexCommand ref
|
||||
reference "eq:wave-function-probability"
|
||||
plural "false"
|
||||
caps "false"
|
||||
noprefix "false"
|
||||
|
||||
\end_inset
|
||||
|
||||
and
|
||||
\begin_inset CommandInset ref
|
||||
LatexCommand ref
|
||||
reference "eq:wave-function"
|
||||
plural "false"
|
||||
caps "false"
|
||||
noprefix "false"
|
||||
|
||||
\end_inset
|
||||
|
||||
gives the final probability function for the entire well:
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
\begin_inset Formula
|
||||
\[
|
||||
P\left(0\leq x\leq x_{0}\right)=\frac{1}{L}\left(x_{0}-\frac{L}{2n\pi}\sin\left(\frac{2n\pi x_{0}}{L}\right)\right)
|
||||
\]
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
Where
|
||||
\begin_inset Formula $x_{0}$
|
||||
\end_inset
|
||||
|
||||
is an arbitrary distance across the well.
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
\begin_inset Newpage pagebreak
|
||||
\end_inset
|
||||
@ -541,7 +1439,7 @@ Probability Intervals
|
||||
|
||||
\end_layout
|
||||
|
||||
\begin_layout Section
|
||||
\begin_layout Part
|
||||
Application of Nanomaterials
|
||||
\end_layout
|
||||
|
||||
|
||||
BIN
coursework.pdf
BIN
coursework.pdf
Binary file not shown.
BIN
probability-plot.png
Normal file
BIN
probability-plot.png
Normal file
Binary file not shown.
|
After 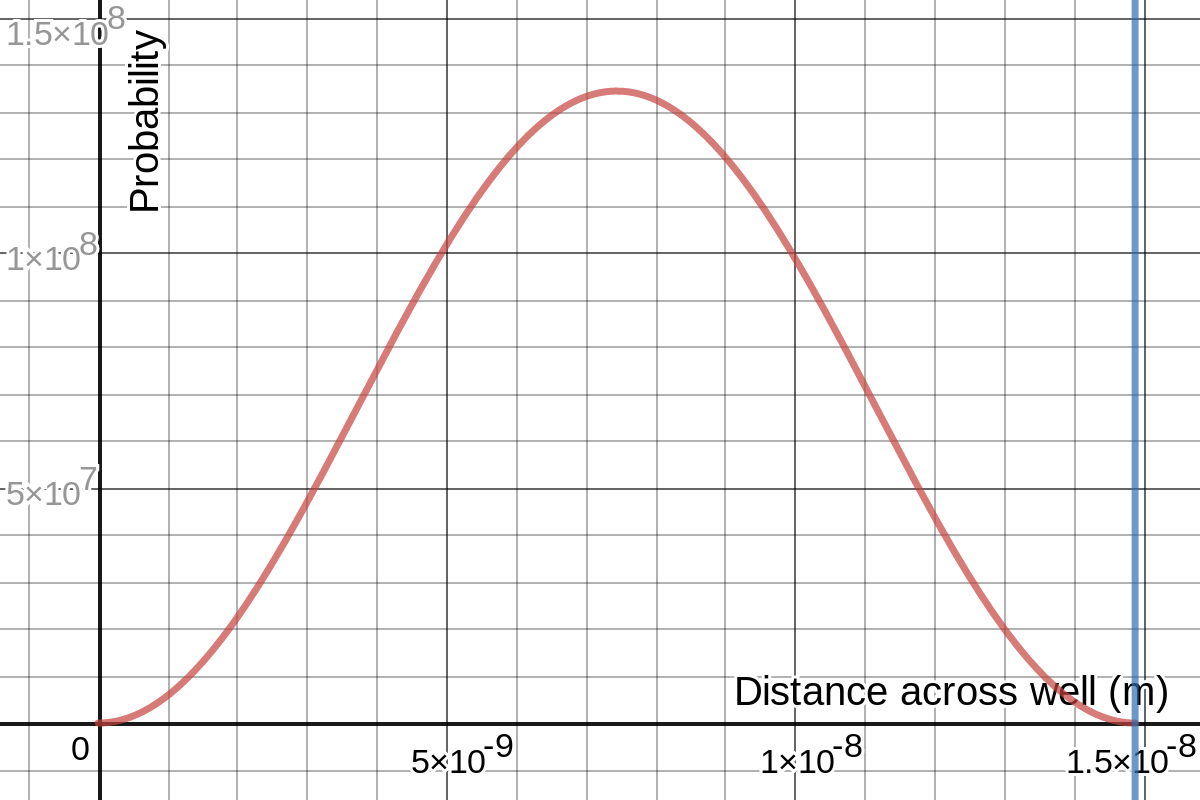
(image error) Size: 73 KiB |
@ -16,5 +16,67 @@ year = "2014-11"
|
||||
@misc{new_semiconductor_materials_archive,
|
||||
title={NSM Archive - Physical Properties of Semiconductors},
|
||||
url={http://matprop.ru/},
|
||||
journal={New Semiconductor Materials Archive}, publisher={Ioffe Institute}
|
||||
journal={New Semiconductor Materials Archive},
|
||||
publisher={Ioffe Institute}
|
||||
}
|
||||
|
||||
@article{aip_complete10.1063/1.322570,
|
||||
abstract = "Very uniform In 0.53 Ga 0.47 As was grown on InP by liquid phase epitaxy. The electron mobility is 8450 cm 2 /V sec at 300 K and 27700 cm 2 /V sec at 77 K. The mobility increases with decreasing temperature from 300 to 77 K in contrast to the results of In 1− x Ga x As grown directly on GaAs by vapor phase epitaxy. The energy gap of this high‐mobility material is 0.750 eV at room temperature.",
|
||||
author = "Takeda, Yoshikazu and Sasaki, Akio and Imamura, Yujiro and Takagi, Toshinori",
|
||||
issn = "0021-8979",
|
||||
journal = "Journal of Applied Physics",
|
||||
language = "eng",
|
||||
number = "12",
|
||||
pages = "5405,5408",
|
||||
publisher = "American Institute of Physics",
|
||||
title = "Electron mobility and energy gap of In 0.53 Ga 0.47 As on InP substrate",
|
||||
volume = "47",
|
||||
year = "1976-12",
|
||||
}
|
||||
|
||||
@article{aip_complete10.1063/1.90860,
|
||||
abstract = "The band-edge effective mass for conduction electrons in Ga x In 1-x As y P 1-y has been determined for several different alloy compositions covering the complete range of alloys grown lattice-matched on InP. Measurements show that the effective mass varies nearly linearly with alloy composition.",
|
||||
author = "Nicholas, R. J. and Portal, J. C. and Houlbert, C. and Perrier, P. and Pearsall, T. P.",
|
||||
issn = "0003-6951",
|
||||
journal = "Applied Physics Letters",
|
||||
keywords = "Galliumarsenid ; Drei-Fuenf-Verbindung ; Indiumphosphid ; Effektive Masse;",
|
||||
language = "eng",
|
||||
number = "8",
|
||||
pages = "492,494",
|
||||
publisher = "American Institute of Physics",
|
||||
title = "An experimental determination of the effective masses for Ga x In 1-x As y P 1-y alloys grown on InP",
|
||||
volume = "34",
|
||||
year = "1979",
|
||||
}
|
||||
|
||||
@article{aip_complete10.1063/1.92393,
|
||||
abstract = "We report the use of optical pumping in p -type Ga x In 1-x As y P 1-y nearly lattice-matched to InP. Analysis of the conduction‐electron spin‐polarized photoluminescence has been used to deduce the valence‐band light‐hole effective mass as a function of alloy composition. Our results are in good agreement with masses calculated using the k·p approximation.",
|
||||
author = "Hermann, Claudine and Pearsall, Thomas P.",
|
||||
issn = "0003-6951",
|
||||
journal = "Applied Physics Letters",
|
||||
keywords = "Halbleiterverbindung ; Galliumarsenid ; Indiumphosphid ; A3-B5-Verbindung ; Optisches Pumpen ; Effektive Masse ; Defektelektron ; Valenzband ; Halbleitersubstrat ; P-Halbleiter ; Leitungselektron ; Photolumineszenz ; Spinorientierung;",
|
||||
language = "eng",
|
||||
number = "6",
|
||||
pages = "450,452",
|
||||
publisher = "American Institute of Physics",
|
||||
title = "Optical pumping and the valence-band light-hole effective mass in Ga x In 1-x As y P 1-y (y approx. 2.2x)",
|
||||
volume = "38",
|
||||
year = "1981",
|
||||
}
|
||||
|
||||
@article{aip_complete10.1063/1.101816,
|
||||
author = "Lin, S. Y. and Liu, C. T. and Tsui, D. C. and Jones, E. D. and Dawson, L. R.",
|
||||
issn = "0003-6951",
|
||||
journal = "Applied Physics Letters",
|
||||
keywords = "Materials Sciencegallium Arsenides ; Holes ; Indium Arsenides ; Cyclotron Resonance ; Effective Mass ; Electronic Structure ; Light Transmission ; Superlattices ; Arsenic Compounds ; Arsenides ; Gallium Compounds ; Indium Compounds ; Mass ; Pnictides ; Resonance;",
|
||||
language = "eng",
|
||||
number = "7",
|
||||
pages = "666,668",
|
||||
publisher = "American Institute of Physics",
|
||||
title = "Cyclotron resonance of two-dimensional holes in strained-layer quantum well structure of (100)In 0.20 Ga 0.80 As/GaAs",
|
||||
volume = "55",
|
||||
year = "1989-08-14",
|
||||
}
|
||||
|
||||
|
||||
|
||||
|
||||
Loading…
x
Reference in New Issue
Block a user