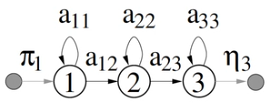Hidden Markov Models - JWMI Github
Rabiner - A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition
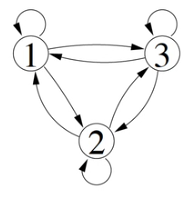
Stochastic sequences of discrete states
Transitions have probabilities
Desired output not always produced the same
P(X|M)=\left(\prod_{t=1}^Ta_{x_{t-1}x_t}\right)\eta_{x_T}a_{x_0x_1}=\pi_{x_1}
Depends only on previous state
P(x_t=j|x_{t-1}=i,x_{t-2}=h,...)\approx P(x_t=j|x_{t-1}=i)
Described by state-transition probabilities
a_{ij}=P(x_t=j|x_{t-1}=i), 1\leq i,j\leq N
\alpha
For N states
N by N matrix of state transition probabilities
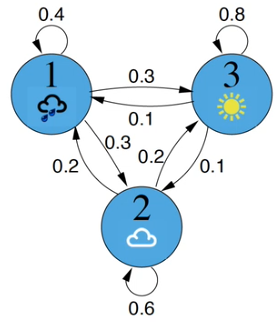
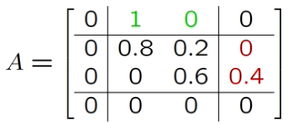
A=\left\{a_{ij}\right\}=\begin{bmatrix} 0.4 & 0.3 & 0.3\\ 0.2 & 0.6 & 0.2 \\ 0.1 & 0.1 & 0.8 \end{bmatrix}rain, cloud, sun across columns and down rows
A=\{\pi_j,a_{ij},\eta_i\}=\{P(x_t=j|x_{t-1}=i)\}
Null states
Entry/exit states
Don't generate observations
\pi_j=P(x_1=j) \space 1 \leq j \leq N
Sub j because probability of kicking off into that state
\eta_i=P(x_T=i) \space 1 \leq i \leq N
Sub i because probability of finishing from that state
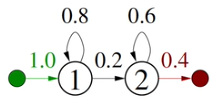
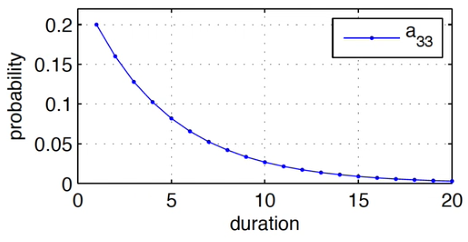
Probability of staying in state decays exponentially
p(X|x_1=i,M)=(a_{ii})^{\tau-1}(1-a_{ii})
Given, a_{33}=0.8
$\times0.8$ repeatedly