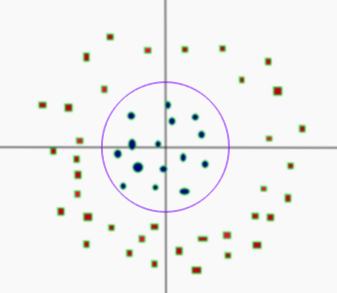
--- tags: - ai - classification --- [Towards Data Science: SVM](https://towardsdatascience.com/support-vector-machines-svm-c9ef22815589) [Towards Data Science: SVM an overview](https://towardsdatascience.com/https-medium-com-pupalerushikesh-svm-f4b42800e989) - Dividing line between two classes - Optimal hyperplane for a space - Margin maximising hyperplane - Can be used for - [Classification](../Classification.md) - SVC - Regression - SVR - Alternative to Eigenmodels for [supervised](../../Learning.md#Supervised) classification - For smaller datasets - Hard to scale on larger sets  - Support vector points - Closest points to the hyperplane - Lines to hyperplane are support vectors - Maximise margin between classes - Take dot product of test point with vector perpendicular to support vector - Sign determines class # Pros - Linear or non-linear discrimination - Effective in higher dimensions - Effective when number of features higher than training examples - Best for when classes are separable - Outliers have less impact # Cons - Long time for larger datasets - Doesn’t do well when overlapping - Selecting appropriate kernel # Parameters - C - How smooth the decision boundary is - Larger C makes more curvy - 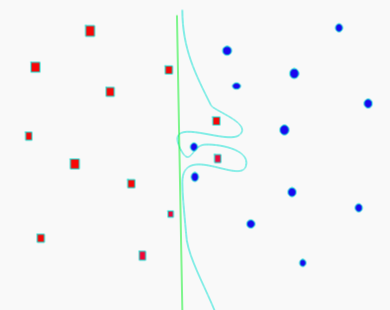 - Gamma - Controls area of influence for data points - High gamma reduces influence of faraway points # Hyperplane $$\beta_0+\beta_1X_1+\beta_2X_2+\cdot\cdot\cdot+\beta_pX_p=0$$ - $p$-dimensional space - If $X$ satisfies equation - On plane - Maximal margin hyperplane - Perpendicular distance from each observation to given plane - Best plane has highest distance - If support vector points shift - Plane shifts - Hyperplane only depends on the support vectors - Rest don't matter 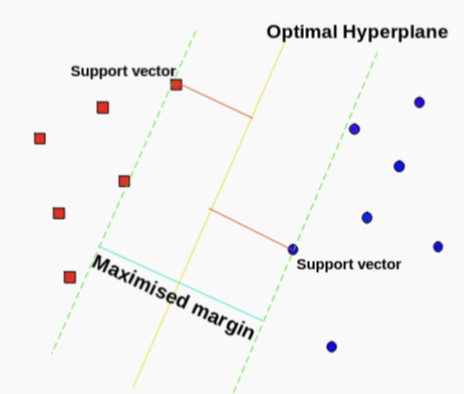 # Linearly Separable - Not linearly separable 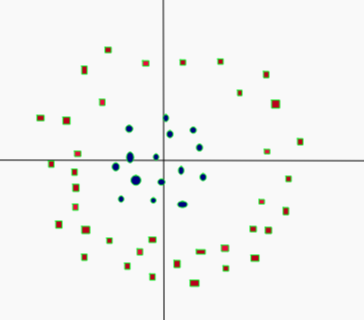 - Add another dimension - $z=x^2+y^2$ - Square of the distance of the point from the origin 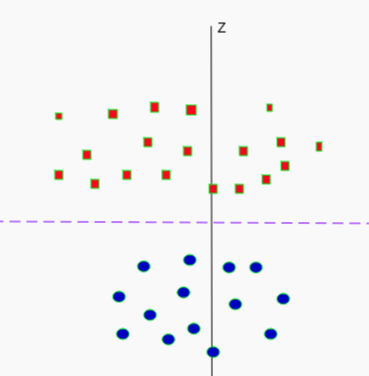 - Now separable - Let $z=k$ - $k$ is a constant - Project linear separator back to 2D - Get circle