proof read part 1, added design drawing
This commit is contained in:
parent
7a3bb3e3b3
commit
0f88146af5
175
coursework.lyx
175
coursework.lyx
@ -140,7 +140,7 @@ f=\frac{c}{\lambda}
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
In order to find the
|
||||
Therefore in order to find the
|
||||
\begin_inset Formula $E$
|
||||
\end_inset
|
||||
|
||||
@ -172,14 +172,15 @@ Returning to the specifications, this allows 1.55μm to be expressed as 1.28x10
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
This energy value will be the same as the total band gap for the well from
|
||||
the first hole energy level to the first electron enery level, shown as
|
||||
This energy value will be the same as the total interband transition for
|
||||
the well from the first confined hole energy level to the first confined
|
||||
electron enery level,
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
\begin_inset Formula
|
||||
\begin{equation}
|
||||
\varSigma E_{g}=E_{1h}+E_{g}+E_{1e}\thickapprox0.8eV\label{eq:Energy-Gap-Sum}
|
||||
E_{g,transition}=E_{1h}+E_{g}+E_{1e}\thickapprox0.8\unit{eV}\label{eq:Energy-Gap-Sum}
|
||||
\end{equation}
|
||||
|
||||
\end_inset
|
||||
@ -221,7 +222,7 @@ status open
|
||||
|
||||
\begin_layout Plain Layout
|
||||
Band structure of an AlGaAs/GaAs/AlGaAs quantum well including discrete
|
||||
energy levels
|
||||
confined energy levels
|
||||
\begin_inset CommandInset citation
|
||||
LatexCommand cite
|
||||
key "ieee_s6824198"
|
||||
@ -253,18 +254,18 @@ name "fig:Well-Band-structure"
|
||||
\begin_inset Formula $E_{g}$
|
||||
\end_inset
|
||||
|
||||
should be the dominant term in this equation and as such in investigating
|
||||
suitable materials, the bulk band gap should be close to but lower than
|
||||
should be the dominant term in this equation and as such when investigating
|
||||
suitable materials the bulk band gap should be close to but lower than
|
||||
0.8eV.
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
None of the binary III-V indium based alloys have bulk band gaps in a suitable
|
||||
range, as such ternary alloys were investigated.
|
||||
Ternary alloys were investigated in order to allow precise control over
|
||||
the lattice constants and band gap by varying the composition ratio.
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
indium gallium arsenide (In
|
||||
Indium gallium arsenide (In
|
||||
\begin_inset script subscript
|
||||
|
||||
\begin_layout Plain Layout
|
||||
@ -327,7 +328,7 @@ Lattice matching is the process of ensuring that two crystalline structures
|
||||
between the two materials.
|
||||
This is particularly important for quantum wells formed through epitaxial
|
||||
growth as strain introduced between such thin layers can cause defects
|
||||
ultimately negatively affecting it's electronic properties.
|
||||
which ultimately negatively affect it's electronic properties.
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
@ -487,7 +488,7 @@ name "tab:Lattice-constants"
|
||||
In order to compute a compound lattice constant for InGaAs, Vegard's law
|
||||
can be applied.
|
||||
Vegard's law provides an approximation for the lattice constant of a solid
|
||||
solution by finding the weighted average the individual lattice constants
|
||||
solution by finding the weighted average of the individual lattice constants
|
||||
by composition ratio and is given by:
|
||||
\end_layout
|
||||
|
||||
@ -742,8 +743,8 @@ Width Calculation
|
||||
\begin_layout Standard
|
||||
Having found two materials that are lattice matched with a suitable band
|
||||
gap value, the final calculation is that of the quantum well width.
|
||||
In order to calculate this value, the equation for energy levels within
|
||||
an infinite quantum well will be used,
|
||||
In order to calculate this value, the equation for confined energy levels
|
||||
within an infinite quantum well will be used,
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
@ -787,7 +788,7 @@ noprefix "false"
|
||||
\begin_layout Standard
|
||||
\begin_inset Formula
|
||||
\[
|
||||
\varSigma E_{g}=0.8\unit{eV}=E_{1h}+E_{g}+E_{1e}=\frac{1^{2}\pi^{2}\text{\emph{ħ}}^{2}}{2m_{h}^{*}L^{2}}+E_{g}+\frac{1^{2}\pi^{2}\text{\emph{ħ}}^{2}}{2m_{e}^{*}L^{2}}
|
||||
E_{g,transition}=0.8\unit{eV}=E_{1h}+E_{g,InGaAs}+E_{1e}=\frac{1^{2}\pi^{2}\text{\emph{ħ}}^{2}}{2m_{h}^{*}L^{2}}+E_{g,InGaAs}+\frac{1^{2}\pi^{2}\text{\emph{ħ}}^{2}}{2m_{e}^{*}L^{2}}
|
||||
\]
|
||||
|
||||
\end_inset
|
||||
@ -797,16 +798,16 @@ noprefix "false"
|
||||
|
||||
\begin_layout Standard
|
||||
With the experimentally determined value for
|
||||
\begin_inset Formula $E_{g}$
|
||||
\begin_inset Formula $E_{g,,InGaAs}$
|
||||
\end_inset
|
||||
|
||||
this equation can be condensed to,
|
||||
this equation becomes
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
\begin_inset Formula
|
||||
\[
|
||||
0.8\unit{eV}=\frac{\pi^{2}\text{\emph{ħ}}^{2}}{2m_{h}^{*}L^{2}}+0.75+\frac{\pi^{2}\text{\emph{ħ}}^{2}}{2m_{e}^{*}L^{2}}
|
||||
0.8\unit{eV}=\frac{\pi^{2}\text{\emph{ħ}}^{2}}{2m_{h}^{*}L^{2}}+0.75\unit{eV}+\frac{\pi^{2}\text{\emph{ħ}}^{2}}{2m_{e}^{*}L^{2}}
|
||||
\]
|
||||
|
||||
\end_inset
|
||||
@ -1064,7 +1065,7 @@ which reduces to a well length of 14.87nm.
|
||||
\end_layout
|
||||
|
||||
\begin_layout Subsection
|
||||
Energy Level Calculations
|
||||
Confined Energy Level Calculations
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
@ -1113,8 +1114,8 @@ E_{1e}=6.65\times10^{-21}\unit{J}=0.041\unit{eV}
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
This equation shows that energy values are proportional to the square of
|
||||
|
||||
This equation shows that confiend energy level values are proportional to
|
||||
the square of
|
||||
\begin_inset Formula $n$
|
||||
\end_inset
|
||||
|
||||
@ -1198,6 +1199,63 @@ E_{2h}=5.45\times10^{-21}\unit{J}=0.034\unit{eV}
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
With the dimensions and first confined energy levels calculated, the final
|
||||
design for the quantum well can be seen in figure
|
||||
\begin_inset CommandInset ref
|
||||
LatexCommand ref
|
||||
reference "fig:quantum-well-design"
|
||||
plural "false"
|
||||
caps "false"
|
||||
noprefix "false"
|
||||
|
||||
\end_inset
|
||||
|
||||
.
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
\begin_inset Float figure
|
||||
wide false
|
||||
sideways false
|
||||
status open
|
||||
|
||||
\begin_layout Plain Layout
|
||||
\align center
|
||||
\begin_inset Graphics
|
||||
filename well-design.png
|
||||
lyxscale 30
|
||||
width 85col%
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\begin_layout Plain Layout
|
||||
\begin_inset Caption Standard
|
||||
|
||||
\begin_layout Plain Layout
|
||||
InP/InGaAs/InP quantum well design
|
||||
\begin_inset CommandInset label
|
||||
LatexCommand label
|
||||
name "fig:quantum-well-design"
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\end_inset
|
||||
|
||||
|
||||
\end_layout
|
||||
|
||||
\begin_layout Section
|
||||
@ -1239,7 +1297,7 @@ with
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
Where
|
||||
Here
|
||||
\begin_inset Formula $A$
|
||||
\end_inset
|
||||
|
||||
@ -1337,6 +1395,17 @@ noprefix "false"
|
||||
\end_inset
|
||||
|
||||
has been set to 1 for the ground state.
|
||||
This function for the first excited state can be seen in figure
|
||||
\begin_inset CommandInset ref
|
||||
LatexCommand ref
|
||||
reference "fig:Probability-plot-n-2"
|
||||
plural "false"
|
||||
caps "false"
|
||||
noprefix "false"
|
||||
|
||||
\end_inset
|
||||
|
||||
.
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
@ -1350,7 +1419,7 @@ status open
|
||||
\begin_inset Graphics
|
||||
filename probability-plot.png
|
||||
lyxscale 30
|
||||
width 100col%
|
||||
width 75col%
|
||||
|
||||
\end_inset
|
||||
|
||||
@ -1396,7 +1465,7 @@ status open
|
||||
\begin_inset Graphics
|
||||
filename probability-plot-with-n-2.png
|
||||
lyxscale 30
|
||||
width 100col%
|
||||
width 75col%
|
||||
|
||||
\end_inset
|
||||
|
||||
@ -1461,7 +1530,16 @@ noprefix "false"
|
||||
|
||||
\end_inset
|
||||
|
||||
gives the final probability function for the entire well:
|
||||
gives the final probability function for a distance across the well from
|
||||
|
||||
\begin_inset Formula $x=0$
|
||||
\end_inset
|
||||
|
||||
to
|
||||
\begin_inset Formula $x=x_{0}$
|
||||
\end_inset
|
||||
|
||||
:
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
@ -1476,15 +1554,7 @@ P\left(0\leq x\leq x_{0}\right)=\frac{1}{L}\left(x_{0}-\frac{L}{2n\pi}\sin\left(
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
Where
|
||||
\begin_inset Formula $x_{0}$
|
||||
\end_inset
|
||||
|
||||
is an arbitrary distance across the well.
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
For an interval across the well, this becomes:
|
||||
For an arbitrary interval across the well, this becomes:
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
@ -1498,6 +1568,37 @@ P\left(a\leq x\leq b\right)=\frac{1}{L}\left(\left(b-a\right)-\frac{L}{2n\pi}\le
|
||||
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
This equation can be utilised in order to find the probability of finding
|
||||
the electron between
|
||||
\begin_inset Formula $2\unit{nm}$
|
||||
\end_inset
|
||||
|
||||
and
|
||||
\begin_inset Formula $4\unit{nm}$
|
||||
\end_inset
|
||||
|
||||
and between
|
||||
\begin_inset Formula $6\unit{nm}$
|
||||
\end_inset
|
||||
|
||||
and
|
||||
\begin_inset Formula $8\unit{nm}$
|
||||
\end_inset
|
||||
|
||||
, the intervals for which can be seen plotted in figure
|
||||
\begin_inset CommandInset ref
|
||||
LatexCommand ref
|
||||
reference "fig:Probability-plot-with-bounds"
|
||||
plural "false"
|
||||
caps "false"
|
||||
noprefix "false"
|
||||
|
||||
\end_inset
|
||||
|
||||
.
|
||||
\end_layout
|
||||
|
||||
\begin_layout Standard
|
||||
\begin_inset Float figure
|
||||
wide false
|
||||
@ -1509,7 +1610,7 @@ status open
|
||||
\begin_inset Graphics
|
||||
filename probability-plot-with-bounds.png
|
||||
lyxscale 30
|
||||
width 100col%
|
||||
width 75col%
|
||||
|
||||
\end_inset
|
||||
|
||||
@ -1576,7 +1677,7 @@ P\left(2\unit{nm}\leq x\leq4\unit{nm}\right)=\frac{1}{14.87\unit{nm}}\left(2\uni
|
||||
\begin_layout Standard
|
||||
\begin_inset Formula
|
||||
\[
|
||||
P\left(2\unit{nm}\leq x\leq4\unit{nm}\right)\thickapprox0.132
|
||||
P\left(2\unit{nm}\leq x\leq4\unit{nm}\right)\thickapprox0.0955
|
||||
\]
|
||||
|
||||
\end_inset
|
||||
@ -1620,7 +1721,7 @@ P\left(6\unit{nm}\leq x\leq8\unit{nm}\right)=\frac{1}{14.87\unit{nm}}\left(2\uni
|
||||
\begin_layout Standard
|
||||
\begin_inset Formula
|
||||
\[
|
||||
P\left(6\unit{nm}\leq x\leq8\unit{nm}\right)\thickapprox0.132
|
||||
P\left(6\unit{nm}\leq x\leq8\unit{nm}\right)\thickapprox0.263
|
||||
\]
|
||||
|
||||
\end_inset
|
||||
|
||||
BIN
coursework.pdf
BIN
coursework.pdf
Binary file not shown.
BIN
well-design.png
Normal file
BIN
well-design.png
Normal file
Binary file not shown.
|
After 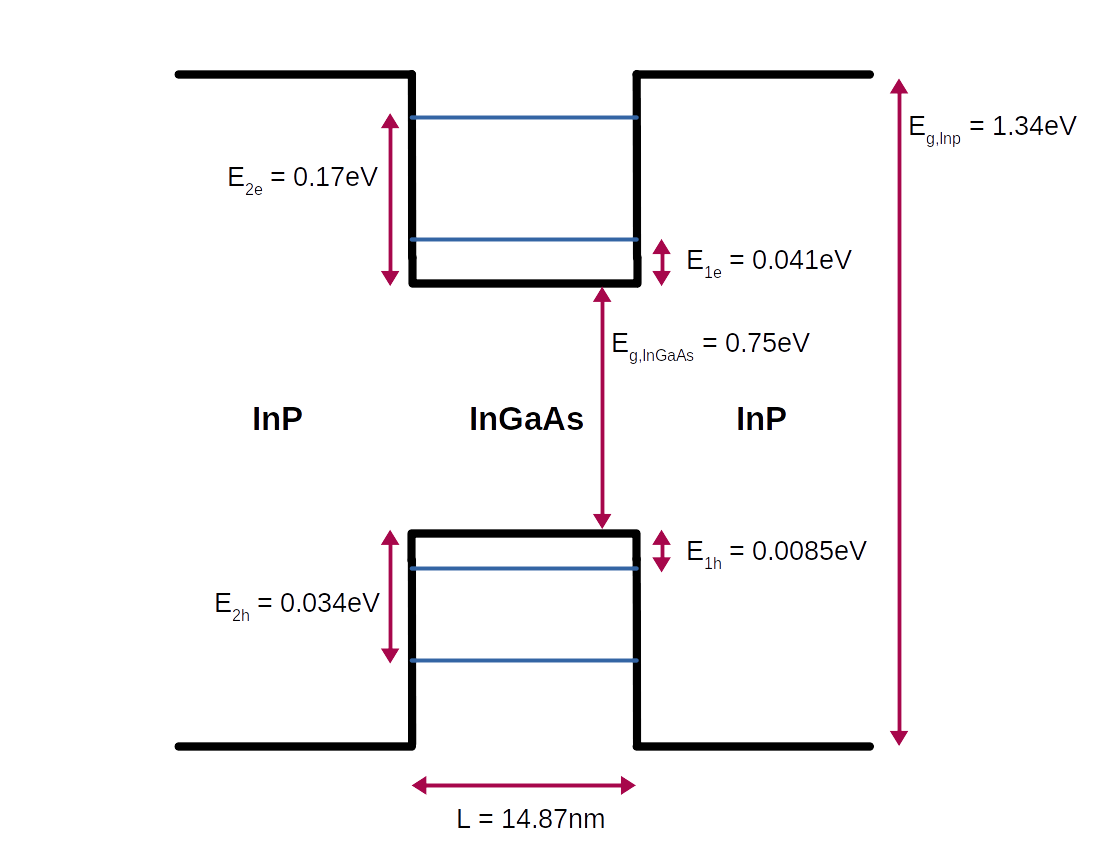
(image error) Size: 70 KiB |
BIN
well-diagram.odg
Normal file
BIN
well-diagram.odg
Normal file
Binary file not shown.
Loading…
x
Reference in New Issue
Block a user